Բնական, ամբողջ և իրական ցուցիչներով աստիճաններ։ Հիմնական հատկությունները

Ընթերցման ժամանակը՝ 15 րոպե

Բնական ցուցիչով աստիճան․

Ցանկացած a թվի n (n>1) բնական ցուցիչով աստիճանը սահմանվում է այսպես՝

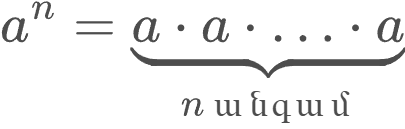
aⁿ -ը կոչվում է a թվի n բնական ցուցիչով աստիճան և սովորաբար կարդացվում է «a-ն բարձրացրած n աստիճան» կամ «a-ի n աստիճան»։ a -ն կոչվում է աստիճանի հիմք, իսկ n -ը՝ աստիճանի ցուցիչ կամ աստիճանացույց։

Եթե n = 1, ապա համարվում է, որ այդ հավասարության աջ մասը հավասար է a -ի, այսինքն՝ a¹ = a :

Եթե a = 0, ապա համարվում է, որ այդ հավասարության աջ մասը հավասար է 0 -ի, այսինքն՝ 0ⁿ = 0 («0» հիմքով բնական ցուցիչով աստիճանի հատկություն)։

Ամբողջ ցուցիչով աստիճան․

Նպատակահարմար է մտցնել հետևյալ երկու պայմանավորվածությունները․

1․ Զրոյից տարբեր ցանկացած a թվի և ցանկացած m բնական թվի համար 1/aᵐ թիվը նշանակել a⁻ᵐ - ով և գրել՝

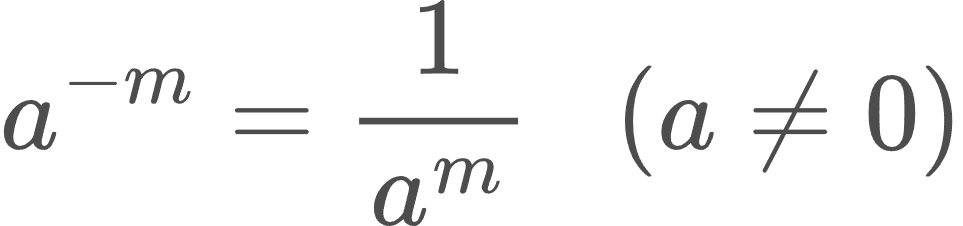
2. Զրոյից տարբեր ցանկացած a թվի համար a⁰ արտահայտությունը համարել 1 և գրել՝

Այսպիսով, aᵐ թիվը, որտեղ a ≠ 0 և m -ը ցանկացած ամբողջ թիվ է, անվանում են ամբողջ ցուցիչով աստիճան։

Դիտողություն։ 0⁰ (0-ի 0 աստիճան) արտահայտությունը իմաստ չունի։ Եթե m -ը բնական թիվ է, ապա 0⁻ᵐ արտահայտությունը նույնպես իմաստ չունի։

Ռացիոնալ ցուցիչով աստիճան․

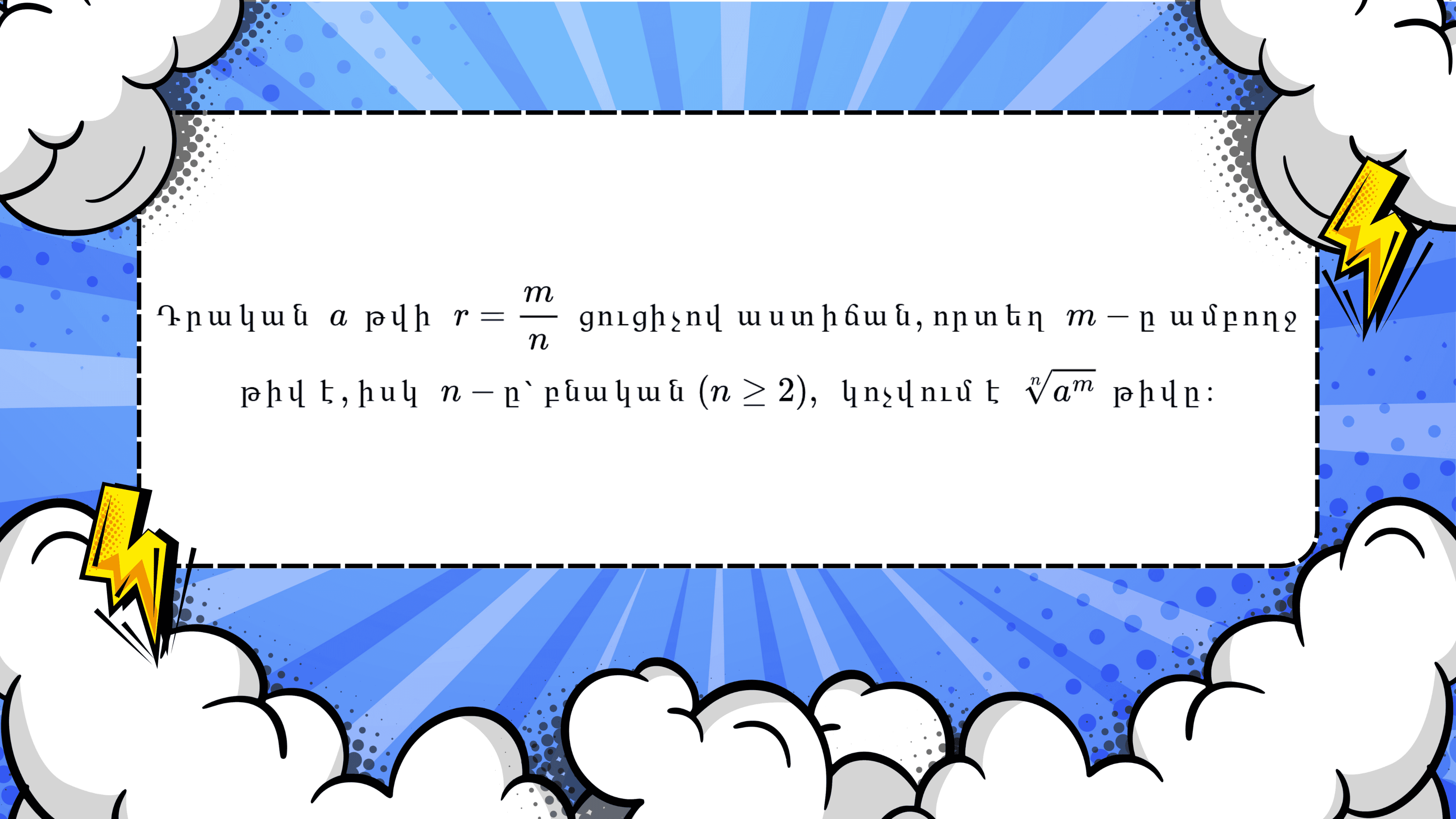
Ըստ սահմանման՝

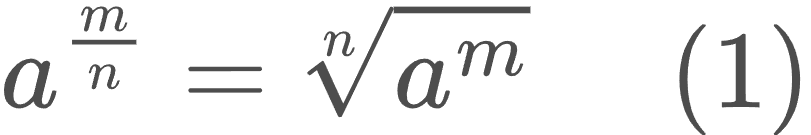
0 թվի աստիճանը որոշված է միայն դրական ցուցիչների դեպքում և ցանկացած r > 0 ռացիոնալ թվի համար 0ʳ = 0:

Դիտողություն 1։ Վերը նշված ձևակերպման մեջ m/n - ը, մասնավորապես, կարող է լինել նաև ամբողջ թիվ։

Դիտողություն 2։ Սահմանումից անմիջապես հետևում է, որ ցանկացած դրական a թվի և ռացիոնալ r -ի համար aʳ թիվը դրական է։

Դիտողություն 3։ Կոտորակի տեսքով տրված ցանկացած բնական n թվի համար m/n = mk / nk: aʳ - ի արժեքը նույնպես կախված չէ r ռացիոնալ թվի գրելաձևից։ Իսկապես, արմատների որոշ հատկություններից օգտվելով կարող ենք գրել, որ․

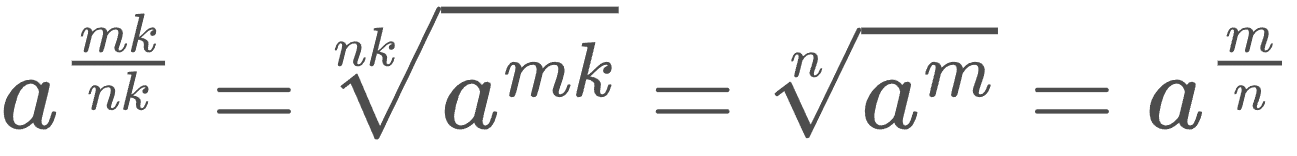
a < 0 դեպքում a թվի կոտորակային ցուցիչով աստիճան չի սահմանվում, և ահա թե ինչու․

Եթե (1) բանաձևը ճիշտ համարենք նաև a < 0 դեպքում, ապա, օրինակ՝ (-8)¹⁄₃ - ի արժեքը կլիներ հավասար ∛-8, այսինքն՝ -2։ Սակայն, մյուս կողմից, 1/3 = 2/6, ուստի ճիշտ կլինի նաև․

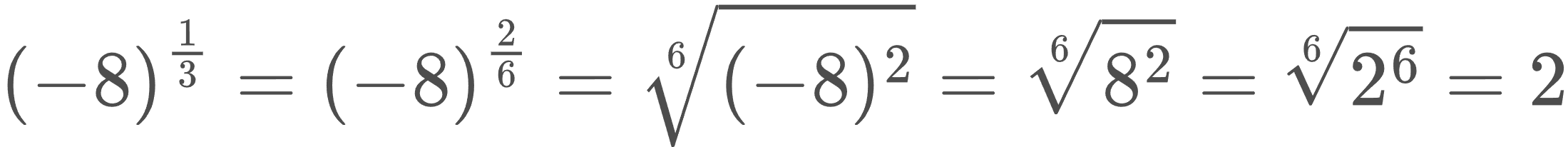
Այսինքն՝ -2 = 2, որն էլ ճիշտ չէ։

Ռացիոնալ ցուցիչով աստիճանի՝ վերը ձևակերպված սահմանվան դեպքում պահպանվում են ամբողջ ցուցիչով աստիճանների հատկությունները (տարբերությունը այն է, որ դրանք ճիշտ են միայն դրական հիմքերի համար)։

Կամայական c և d ռացիոնալ թվերի համար՝

1․ եթե a > 1 և c > d, ապա aᶜ > aᵈ ,

2. եթե 0 < a < 1 և c > d, ապա aᶜ < aᵈ :

Իռացիոնալ ցուցիչով աստիճան․

Հայտնի է, որ ռացիոնալ և իռացիոնալ թվերը միասին անվանում են իրական թվեր։ Իրական թվերը բաղկացած են տասնորդական կոտորակներից․ վերջավոր և անվերջ պարբերական տասնորդական կոտորակներից (ռացիոնալ թվեր) և անվերջ ոչ պարբերական տասնորդական կոտորակներից (իռացիոնալ թվեր)։ Մենք արդեն գիտենք, թե ինչպես է սահմանվում aˣ թիվը, երբ x -ը ռացիոնալ թիվ է։ Հիմա եկեք պարզենք, թե ինչպես է որոշվում aˣ թիվը, եթե x -ը իռացիոնալ է։ Որպեսզի դրական թվի կամայական իրական ցուցիչով աստիճանը լինի որոշված, մնում է սահմանել դրական թվի իռացիոնալ ցուցիչով աստիճանը։

Թիվը, որը կարելի է գրել անվերջ ոչ պարբերական կոտորակի տեսքով կոչվում է իռացիոնալ թիվ: Այսինքն, իռացիոնալ են կոչվում այն թվերը, որոնք չեն կարող ներկայացվել m/n կոտորակի տեսքով, որտեղ m -ը ամբողջ թիվ է, իսկ n -ը՝ բնական։ Սակայն դրանց արժեքները կարելի է մոտարկել տասնորդական կոտորակների միջոցով։ Ավելին, որքան շատ թվանշաններ վերցնենք ստորակետից հետո, այնքան ավելի ճշգրիտ կստանանք արժեքը։

Օրինակ՝ տեսնենք, թե ինչպես է որոշվում 2^√3 (2 -ի √3 աստիճան) թիվը։

Ինչպես գիտենք, √3 -ը իռացիոնալ թիվ է, որը ներկայացվում է անվերջ ոչ պարբերական տասնորդական կոտորակի տեսքով․ √3 = 1,73205…

Դիտարկենք √3 թվի տասնորդական մոտարկումների հաջորդականությունը․

1 ; 1,7 ; 1,73 ; 1,732 ; ․․․

Ակնհայտ է, որ որքան շատ թվանշաններ վերցնենք ստորակետից հետո, այնքան արդյունքը էլ ավելի կմոտենա √3 թվի ճշգրիտ արժեքին։ Այդ դեպքում ասում են, որ տասնորդական կոտորակների հաջորդականությունը զուգամիտում է √3 -ին։

Քանի որ հաջորդականության յուրաքանչյուր անդամ ռացիոնալ թիվ է, որոշված կլինի նաև հետևյալ թվերի հաջորդականությունը.

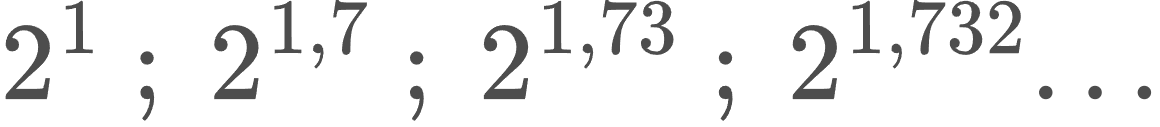
Ստացված հաջորդականությունը չի նվազում և սահմանափակ է վերևից (օրինակ՝ 2² = 4 թվով),հետևաբար, այն ունի սահման։ Այդ սահմանի արժեքն էլ կոչվում է 2 թվի √3 ցուցիչով աստիճան և նշանակվում՝ 2^√3։

Նույն մոտեցումն են ցույց տալիս նաև ընդհանուր դեպքում՝ aˣ -ը, որտեղ a>0 և x -ը իռացոնալ թիվ է, որոշելիս։ x թվի համար կազմում են x₁, x₂, x₃, … ռացիոնալ թվերի հաջորդականություն, որը զուգամիտում է x -ին, այսինքն՝

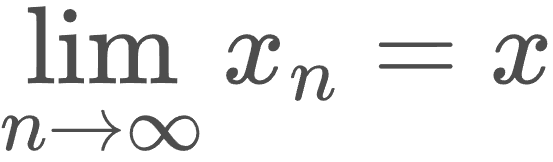
Այնուհետև դիտարկում են a^(x₁) ; a^(x₂) ; a^(x₃) ; … հաջորդականությունը։ Կարելի է ապացուցել, որ այս հաջորդականությունը զուգամիտում է դրական մի c թվի, որը կախված չէ x թվին զուգամիտող x₁, x₂, x₃, … ռացիոնալ թվերի հաջորդականության ընտրությունից, այսինքն՝

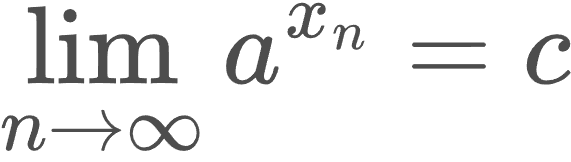
c թիվը անվանում են x իրական ցուցիչով դրական a թվի աստիճան և նշանակում aˣ -ով։

Դիտողություններ։

1. a>1 և x< 0 դեպքում aˣ -ը որոշվում է այսպես՝

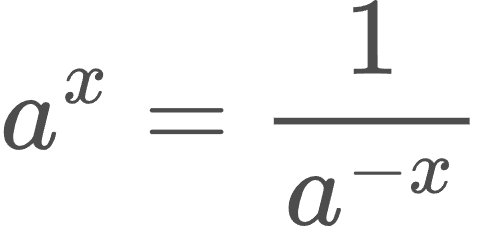
2. 0 < a < 1 դեպքում 1/a > 1, և կամայական իրական x -ի համար aˣ -ը կարող ենք որոշել այսպես՝

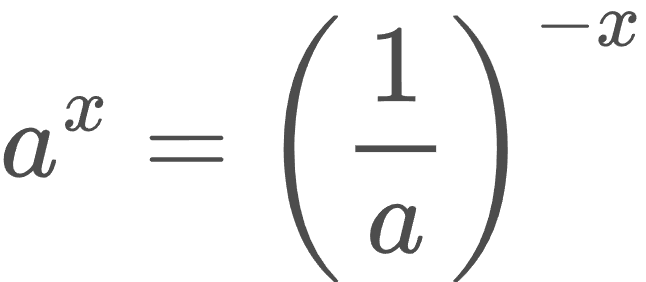
3. a = 1 դեպքում 1ˣ = 1 կամայական իրական x -ի համար։

4. a = 0 դեպքում 0ˣ = 0 կամայական դրական x -ի համար։

Այսպիսով՝ aˣ -ը դրական a հիմքի դեպքում որոշված է բոլոր իրական x -երի համար։

Ընդհանրապես, a∈ℝ, x∈ℝ և m∈ℕ, n∈ℕ թվերի համար ճիշտ են ստորև բերված հատկությունները․

Այս ամենից պարզ դարձավ, որ.

1. ցանկացած a հիմքով (a∈ℝ) աստիճանը որոշված է միայն բնական ցուցիչների համար,
2. ցանկացած a ≠ 0 հիմքով աստիճանը որոշված է միայն «0» և բացասական ամբողջ ցուցիչների համար,
3. ցանկացած a ≥ 0 հիմքով աստիճանը որոշված է միայն դրական կոտորակային ցուցիչների համար,
4. ցանկացած a > 0 հիմքով աստիճանը որոշված է իրական (կամ բացասական կոտորակային) ցուցիչների համար,
5. ցանկացած a < 0 հիմքով աստիճանը որոշված է միայն ամբողջ ցուցիչների համար,
6. «0» հիմքով (a = 0) աստիճանը որոշված է միայն դրական իրական ցուցիչների համար,
7. «1» հիմքով (a = 1) աստիճանը որոշված է ցանկացած իրական ցուցիչների համար։

Հիմնական հատկությունները

a∈ℝ, b∈ℝ, m∈ℤ, n∈ℤ և x∈ℝ, y∈ℝ թվերի համար ճիշտ են ստորև բերված հատկությունները․

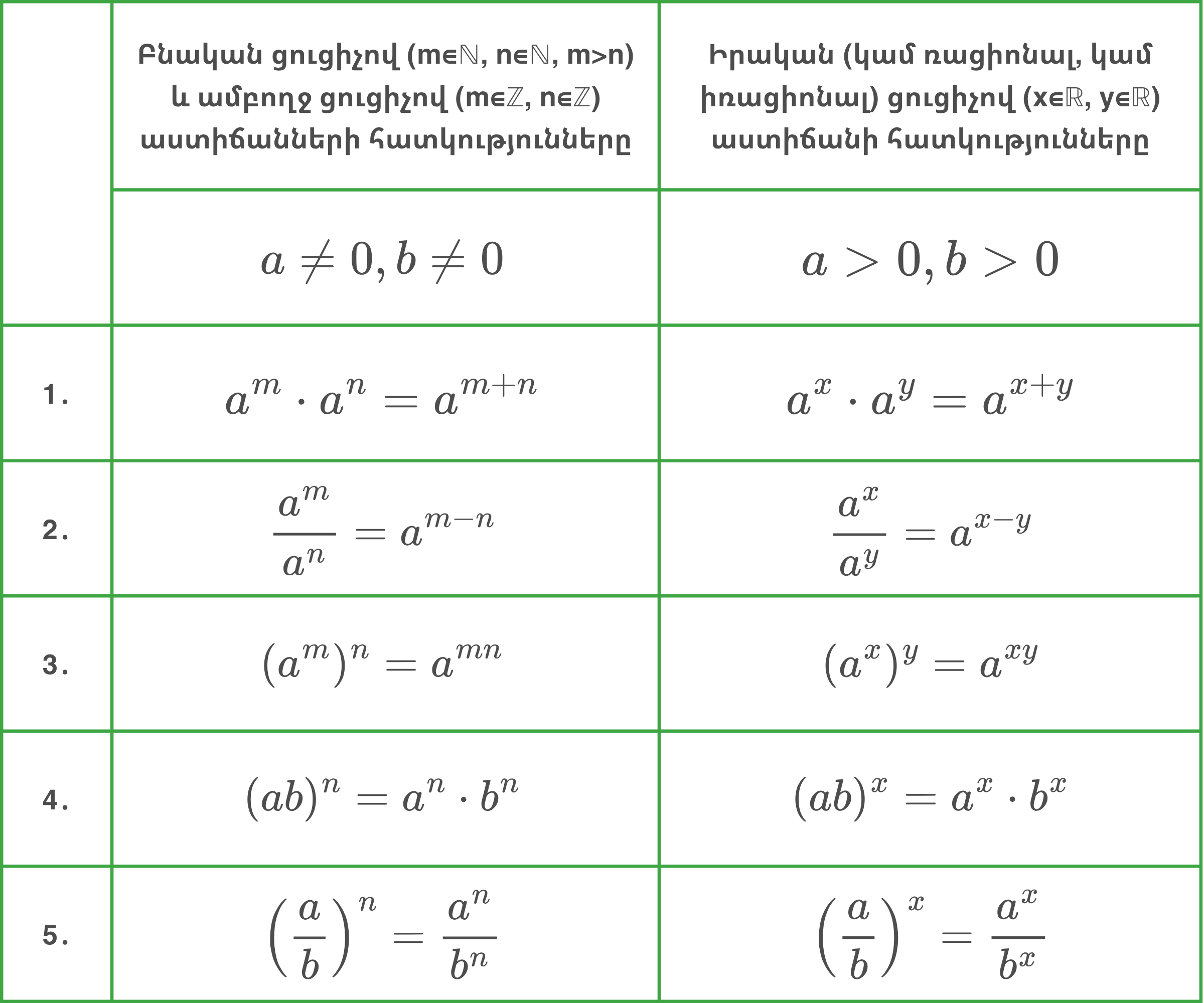
6․ աստիճանների համեմատության մասին

•  եթե a > 1 և x > y, ապա aˣ > aʸ ,
•  եթե 0 < a < 1 և x > y, ապա aˣ < aʸ ,
•  եթե a > b > 0 և x > 0, ապա aˣ > bˣ ,
•  եթե a > b > 0 և x < 0, ապա aˣ < bˣ :

Շնորհակալություն ուշադրության համար