Համեմատականություն։ Հիմնական հատկությունները և տեսակները

Ընթերցման ժամանակը՝ 6 րոպե

Համեմատականության հատկությունները․ հիմնական հատկությունը

Համեմատականության եզրային անդամների արտադրյալը հավասար է միջին անդամների արտադրյալին։

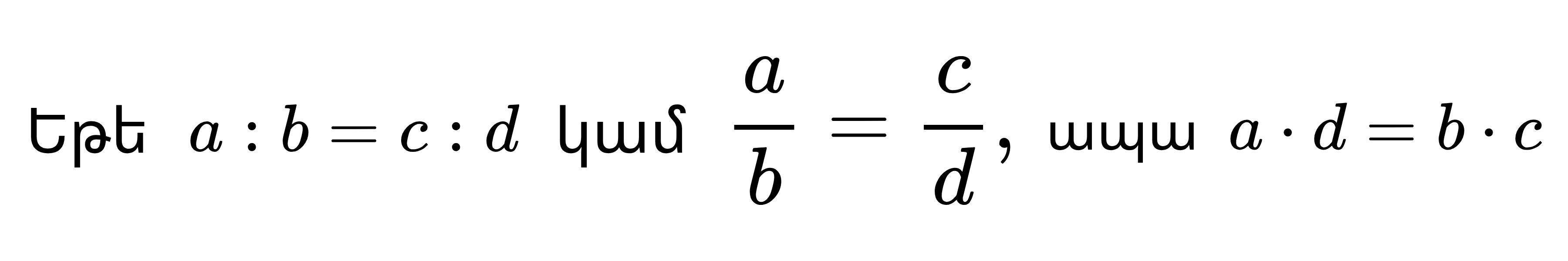
Օրինակ՝ 15 ։ 9 = 5 ։ 3, ապա 15 ⋅ 3 = 9 ⋅ 5

Այլ հատկություններ․

a : b = c : d համեմատականության համար, որտեղ a-ն, b-ն, c-ն և d-ն 0-ից տարբեր իրական թվեր են, ճիշտ են հետևյալ հավասարությունները՝

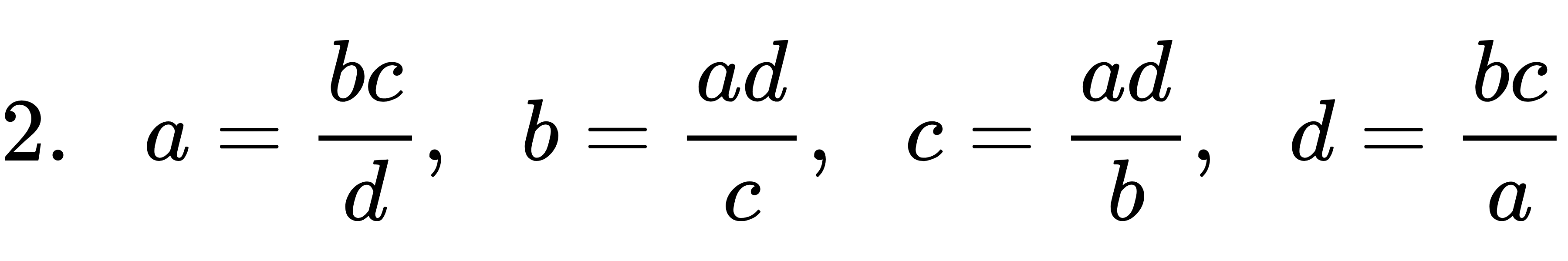
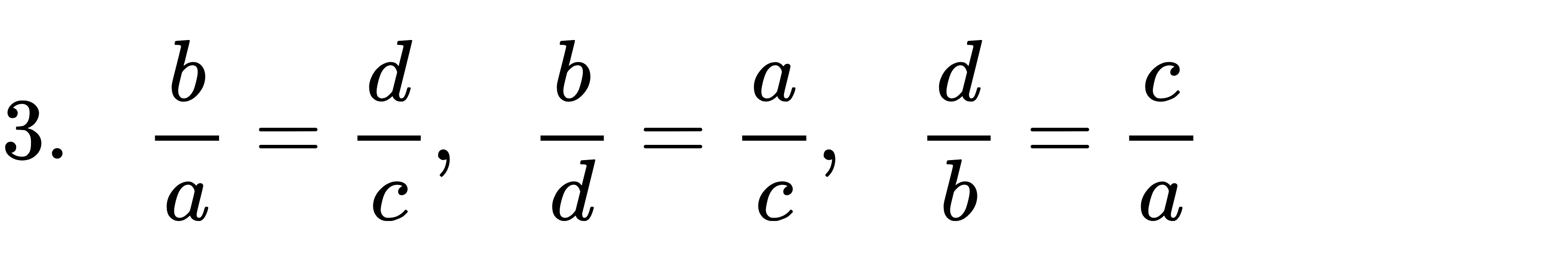
Եթե համեմատականության անդամներից մեկն անհայտ է, ապա այն գտնելու գործողությունը կոչվում է համեմատականության լուծում։

Օրինակ՝ 2 : 5 = 4 : x

Ըստ համեմատականության հիմնական հատկության՝

2 ⋅ x = 5 ⋅ 4, ուստի՝ x ⋅ 2 = 20, x = 20 : 2, x = 10

Համեմատականության տեսակները․ ուղիղ և հակադարձ համեմատականություններ

Երկու մեծություններ անվանում են ուղիղ համեմատական, եթե դրանցից մեկը որևէ անգամ մեծացնելիս (փոքրացնելիս) մյուսը նույնպես մեծանում (փոքրանում) է նույնքան անգամ։

Ուղիղ համեմատականությունը արտահայտվում է y = kx բանաձևով, որտեղ k-ն հաստատուն թիվ է (k = const) և կոչվում է ուղիղ համեմատականության գործակից։

y = kx բանաձևից ստացվում է, որ y : x = k, ուստի ուղիղ համեմատականությունը նաև հասատատուն հարաբերությամբ համեմատականություն է։

Օրինակ.

Հավասարաչափ շարժվելով՝ ավտոմեքենան 100կմ անցնելու համար ծախսեց 8լ բենզին: Որքա՞ն բենզին կծախսի ևս 250կմ անցնելու համար:

100 կմ — 8 լ

250 կմ — x լ

Ըստ խնդրի պայմանի՝ ճանապարհը մեծացել է 250 ։ 100 = 5 : 2 = 2,5 անգամ։ Ուստի հաշվի առնելով, որ հաստատուն արագության դեպքում ճանապարհն ու ծախսած բենզինի քանակը ուղիղ համեմատական մեծություններ են, 2,5 անգամ էլ պետք է մեծանա ծախսվող բենզինի քանակը։ Այսպիսով՝

x : 8 = 250 : 100, որտեղից էլ՝ x = 2,5 ⋅ 8 =  20 (լ)։

Երկու մեծություններ անվանում են հակադարձ համեմատական, եթե դրանցից մեկը որևէ անգամ մեծացնելիս (փոքրացնելիս) մյուսը նույնպես փոքրանում (մեծանում) է նույնքան անգամ։

Հակադարձ համեմատականությունը արտահայտվում է y = k/x բանաձևով, որտեղ k-ն հաստատուն թիվ է և կոչվում է հակադարձ համեմատականության գործակից։

y = k/x բանաձևից ստացվում է, որ y ⋅ x = k, ուստի հակադարձ համեմատականությունը նաև հասատատուն արտադրյալով համեմատականություն է։

Օրինակ.

Միևնույն արտադրողականությամբ աշխատող 6 բանվոր պարիսպը կարող են շարել 30 օրում։ Քանի՞ օրում այդ պարիսպը կշարեն այդ նույն արտադրողականությամբ աշխատող 10 բանվորը։

6 — 30 օր

10 — t օր

Հաշվի առնելով, որ բանվորների քանակը հակադարձ համեմատական է աշխատանքի տևողությանը, կստանանք՝

t : 30 = 6 : 10, որտեղից էլ՝ t = (6 ⋅ 30) : 10 = 18 (օր)։

Դիտողություն․ հակադարձ համեմատականությունը չի աշխատում, եթե աշխատողների արդյունավետությունը տարբեր է։

Խնդիրներ լուծելու ընդհանրական քայլեր․

1․ Որոշել՝ ուղիղ է համեմատականությունը, թե հակադարձ,

2․ Գտնել համեմատականության գործակիցը՝ k-ն,

3․ Կիրառել համապատասխան բանաձևը՝ անհայտը գտնելու համար։

Խորհուրդ. Խնդիրներ լուծելիս միշտ ստուգեք՝ արդյո՞ք մեծությունների արտադրյալը հաստատուն է:

Ինչու՞ է կարևոր ստուգել արտադրյալը․

Սխալներից խուսափելու համար. Որոշ խնդիրներում մեծությունները կարող են թվալ հակադարձ համեմատական, բայց չլինել (օրինակ՝ եթե աշխատանքի ծավալը փոխվում է): Արտադրյալի հաստատուն լինելը վկայում է, որ խնդիրը հակադարձ համեմատականությանն է վերաբերում:

Շնորհակալություն ուշադրության համար