Իրական թվի բացարձակ արժեքը կամ մոդուլը

Ընթերցման ժամանակը՝ 14 րոպե

Կամայական x իրական թվի բացարձակ արժեքը կամ մոդուլը նշանակվում է |x| և սահմանվում է հետևյալ կերպ՝

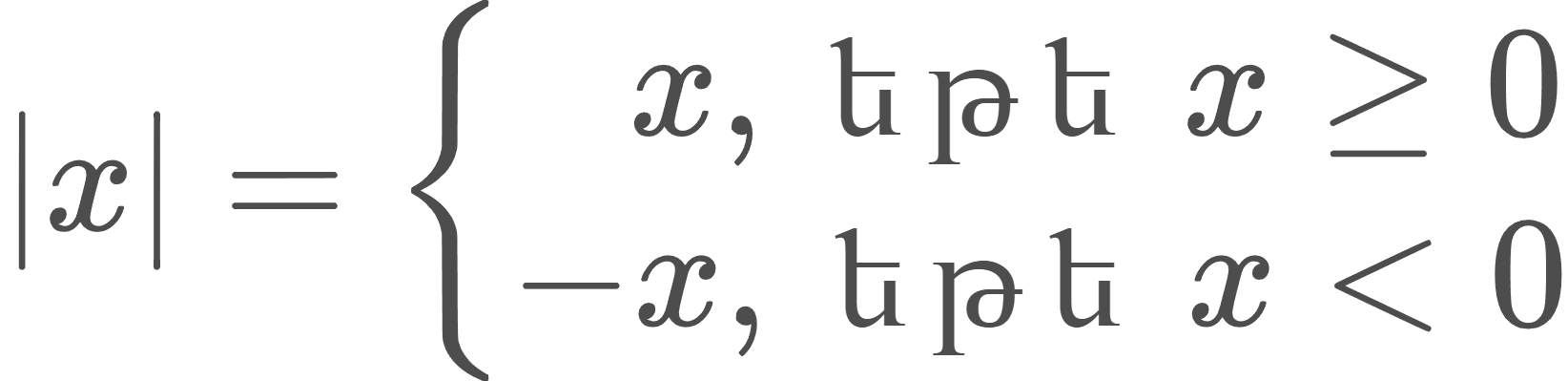
Սահմանումից հետևում է, որ կամայական իրական թվի մոդուլը կա՛մ դրական է, կա՛մ հավասար է զրոյի, բայց ոչ մի դեպքում չի կարող բացասական լինել։

Երկրաչափության տեսանկյունից, իրական թվի բացարձակ արժեքը թվային ուղղի վրա այդ թվին համապատասխանող կետի հեռավորությունն է հաշվարկման սկզբնակետից՝ զրոյից։

Այն ուղիղը, որի համար ընտրված են հաշվարկման սկզբնակետ, դրական ուղղություն և միավոր հատված, կոչվում է թվային ուղիղ։ Ընդունված է թվային ուղիղը պատկերել հորիզոնական գծով և 1-ը պատկերել 0-ից աջ։ 0-ի և 1-ի միջև հեռավորությունը համարվում է չափման միավոր։ Այդ իսկ պատճառով, դրական թվերը պատկերվում են զրոյից աջ, իսկ բացասական թվերը՝ զրոյից ձախ։ Այսինքն՝ զրոն բաժանում է դրական և բացասական թվերի բազմությունները։

Դրական ռացիոնալ a թիվը թվային ուղղի (առանցքի) վրա պատկերվում է 0-ից a միավոր հեռավորության վրա կետով, նույն կողմում, ինչ որ 1-ը։ Բացասական ռացիոնալ b թիվը պատկերվում է հակադիր կողմում՝ 0-ից |b| = -b հեռավորությամբ։ Այսպիսով՝ հակադիր ռացիոնալ թվերը թվային ուղղի վրա պատկերվում են 0-ի տարբեր կողմերում, 0-ից նույն հեռավորությամբ։

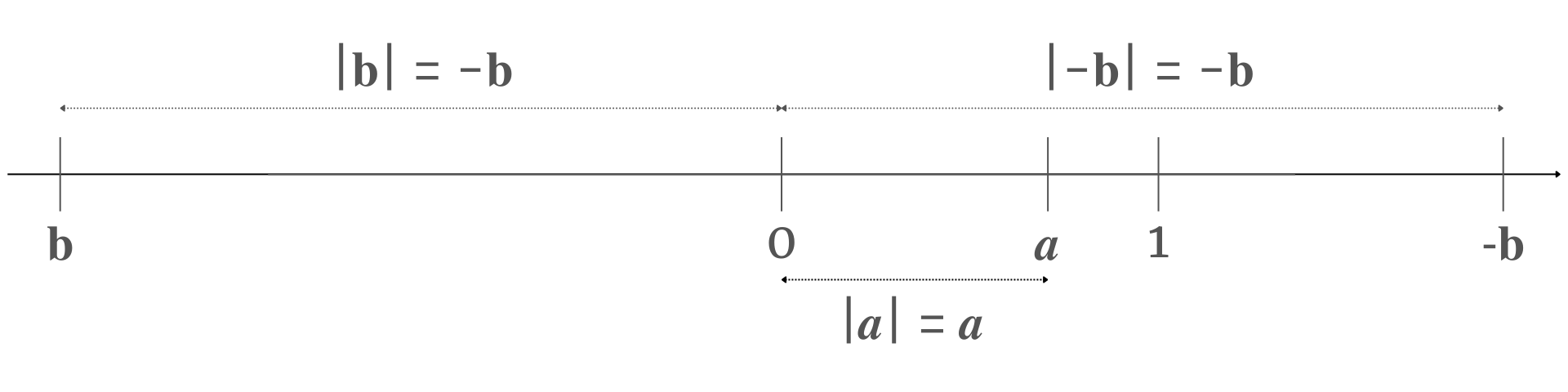
Թվային ուղղի կամայական կետի համապատասխանում է մի իրական թիվ և հակառակը․ կամայական իրական a թվի թվային ուղղի վրա համապատասխանում է մի կետ։ Այն գտնվում է սկզբնակետից |a| հեռավորության վրա՝ սկզբնակետից աջ, եթե a-ն դրական է և ձախ, եթե a-ն բացասական է։

Ընդհանրապես, երկու իրական թվերի տարբերության մոդուլը թվային առանցքի վրա այդ թվերին համապատասխանող կետերի միջև հեռավորությունն է։

Թվային ուղղի M կետին համապատասխանող m թիվը երբեմն անվանում են M կետի կոորդինատ։ Հետևաբար թվային ուղիղն անվանում են նաև կոորդինատային ուղիղ։

Երկու դրական թվերից ավելի մեծ է այն մեկը, որի բացարձակ արժեքն ավելի մեծ է։

Օրինակ՝ |7| > |5| (կարելի է օգտվել երկրաչափական իմաստից) => 7 > 5։

Երկու բացասական թվերից ավելի մեծ է այն մեկը, որի բացարձակ արժեքն ավելի փոքր է։

Օրինակ՝ |-5| < |-7| (նույն պատճառով) => -5 > -7 ։

Իրական a կամ b թվի մոդուլի համար ճիշտ են հետևյալ հատկությունները․

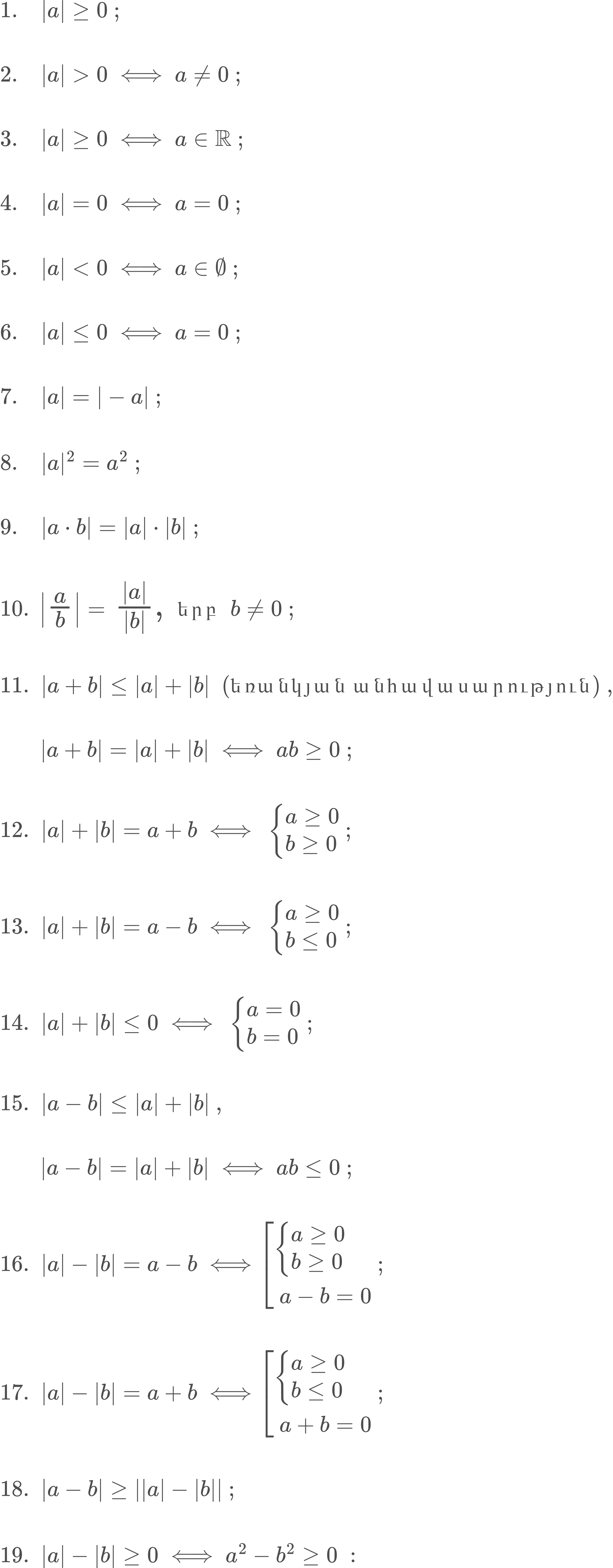
Մոդուլ պարունակող հավասարումներ և անհավասարումներ․

Մոդուլ պարունակող հավասարումներ և անհավասարումներ լուծելիս օգտակար է իմանալ ստորև բերված որոշ հատկություններ։

Կամայական իրական x և y թվերի համար ճիշտ են հետևյալ հատկությունները․

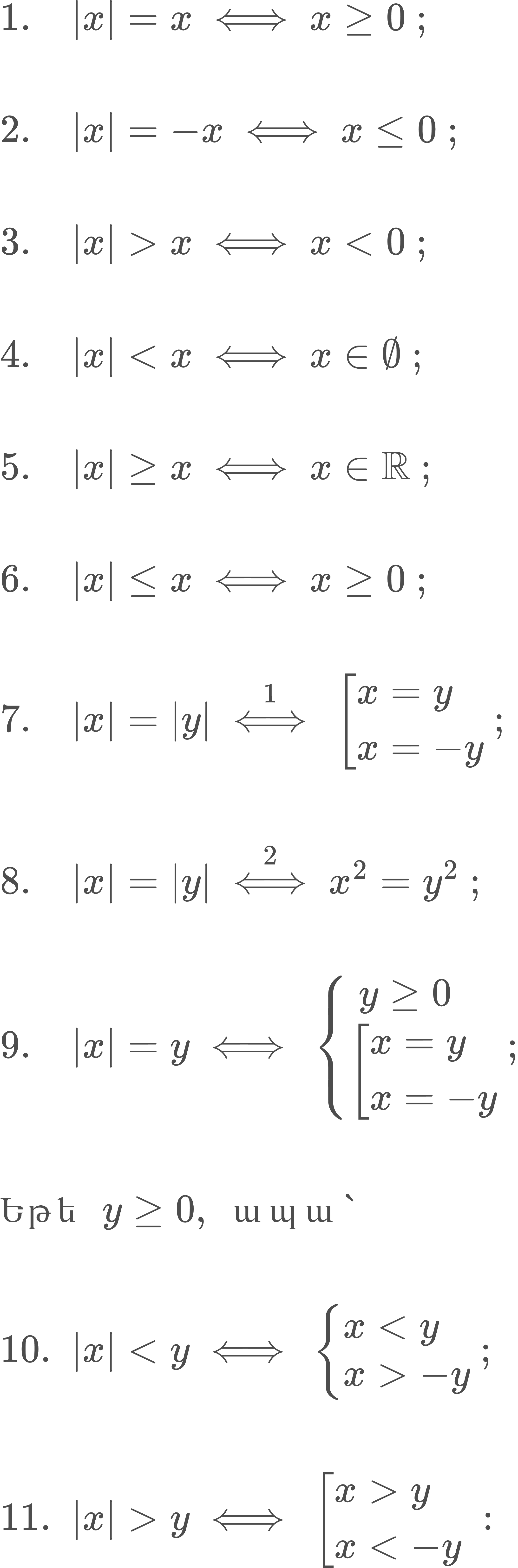
Եթե մոդուլ պարունակող հավասարումները և անհավասարումները x-ի և y-ի փոխարեն պարունակում են փոփոխականով արտահայտություններ, ապա դրանք լուծվում են համանման ձևով և համաձայն վերոթվարկված հատկությունների։

|f(x)| = 0, |f(x)| ≥ 0, |f(x)| ≤ 0 տեսքի հավասարումների և անհավասարումների լուծումը։

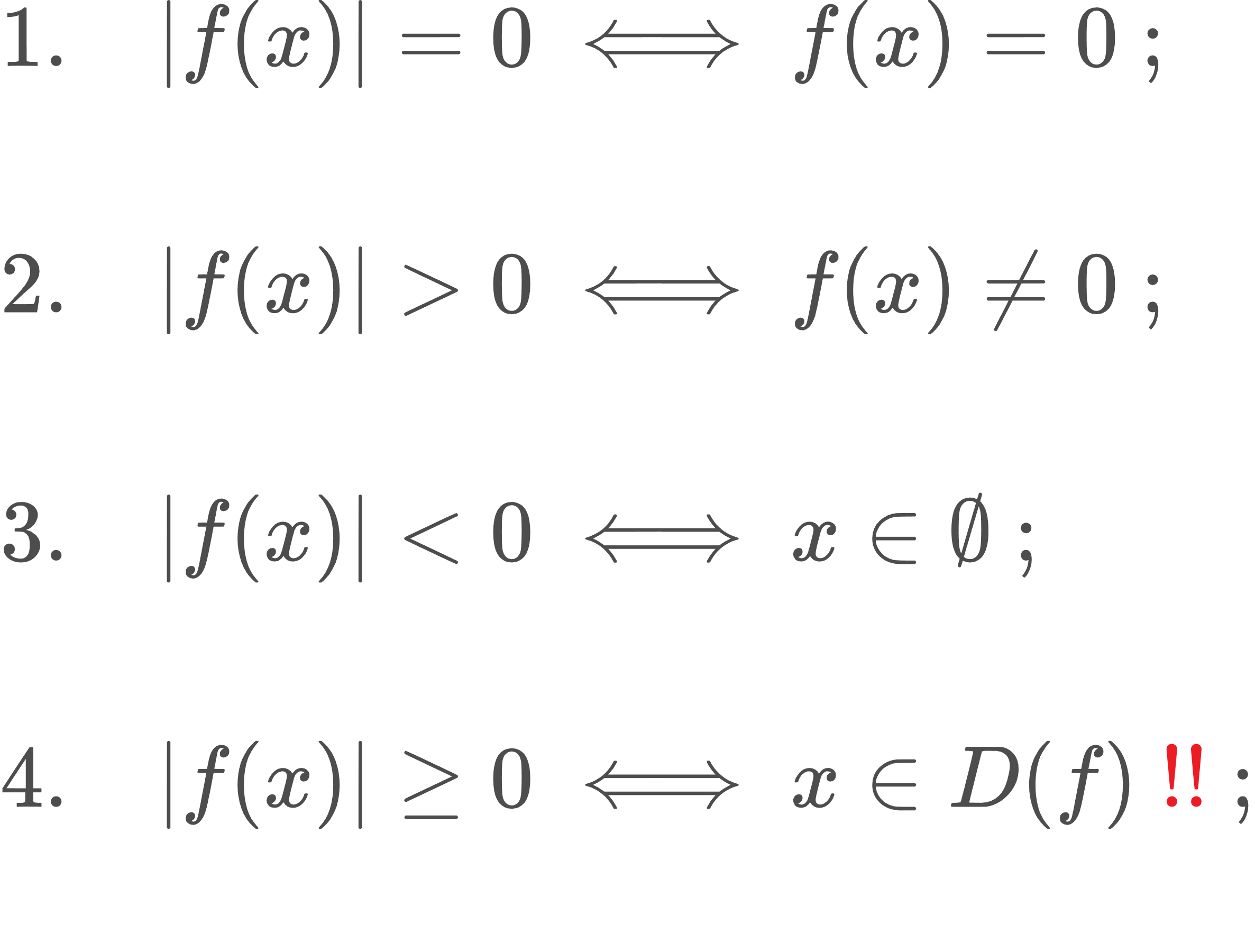
Դիտողություն։ Չենք կարող պնդել, որ x∈ℝ, քանի որ f ֆունկցիան կարող է որոշված չլինել (-∞ ; ∞)-ում, այլ որոշված լինել ինչ-որ (a ; b) միջակայքում։

|f(x)| = a տեսքի հավասարումների լուծումը։

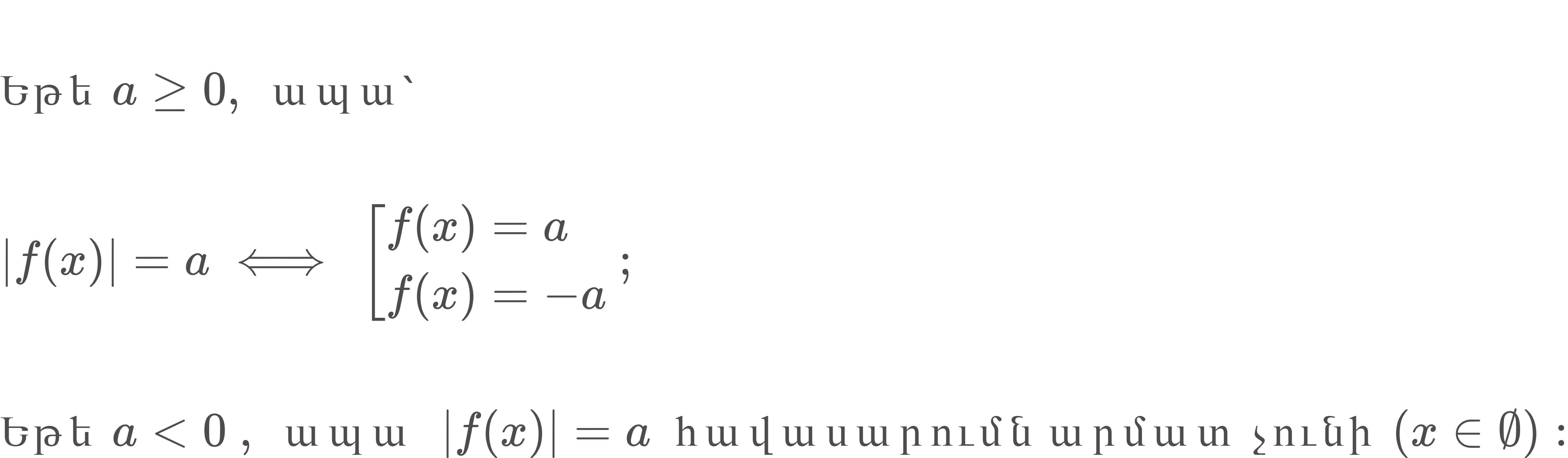
|f(x)| ≥ a, |f(x)| ≤ a տեսքի անհավասարումների լուծումը։

|f(x)| = g(x) տեսքի հավասարումների լուծումը։

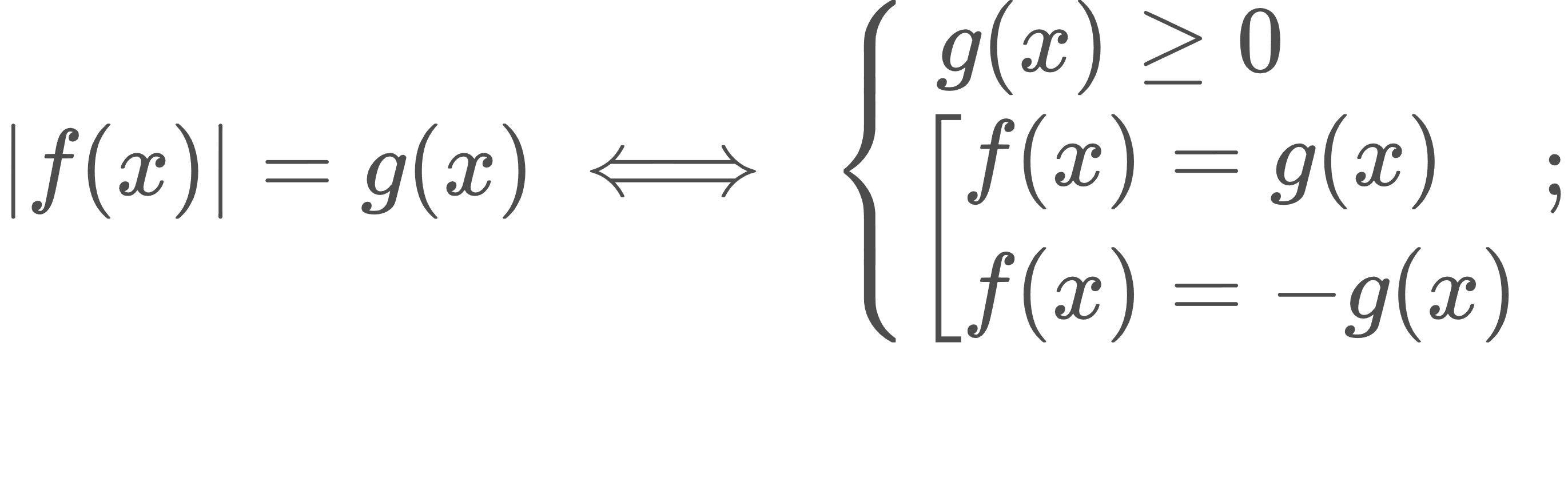
|f(x)| > g(x), |f(x)| < g(x) տեսքի անհավասարումների լուծումը։

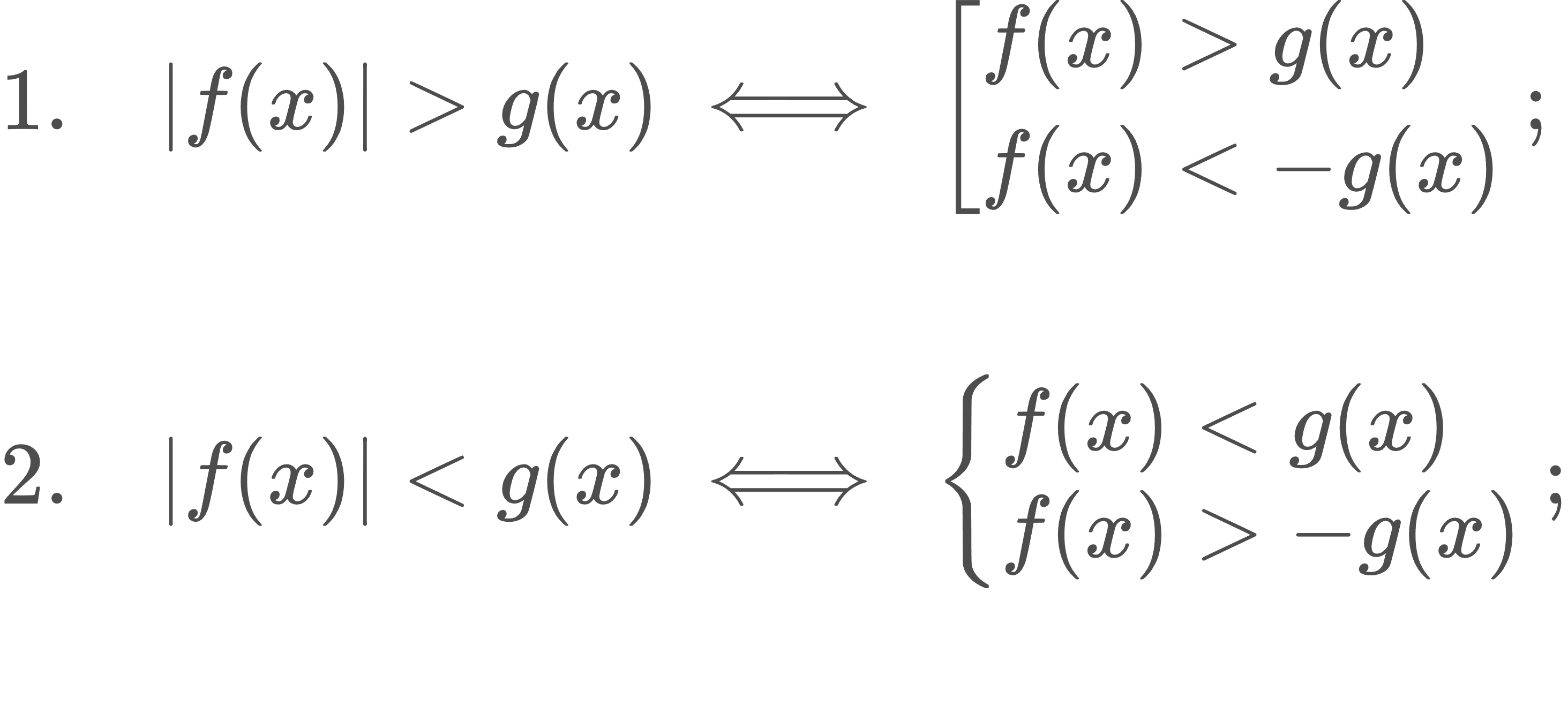
|f(x)| = |g(x)| տեսքի հավասարումների լուծումը։

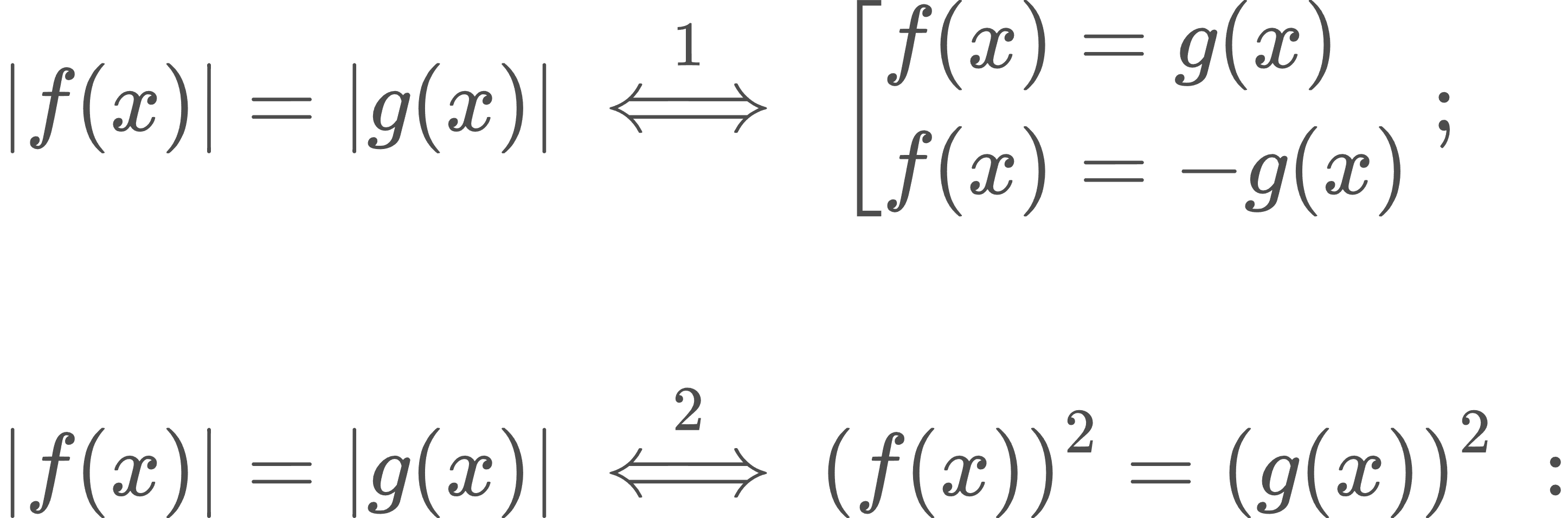
|f(x)| > |g(x)|, |f(x)| < |g(x)| տեսքի անհավասարումների լուծումը։

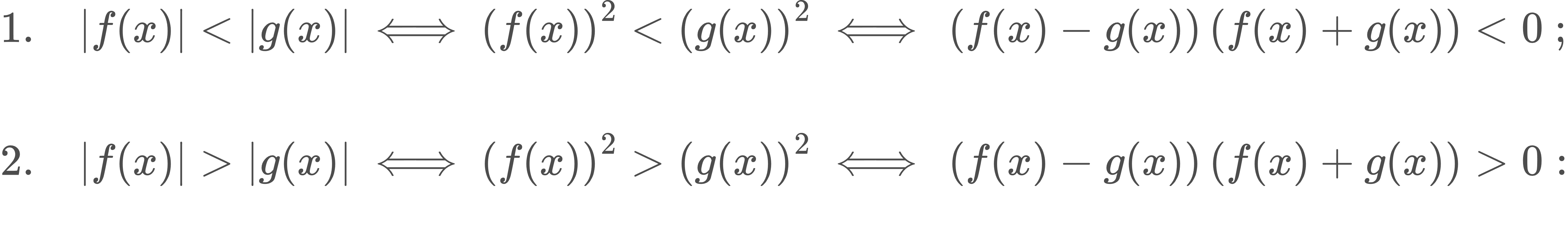
|f₁(x)|+|f₂(x)|+․․․+|fₙ(x)| = a,

|f₁(x)|+|f₂(x)|+․․․+|fₙ(x)| > a

տեսքի հավասարումների և անհավասարումների լուծումը։

Այս տեսքի հավասարումները և անհավասարումները հարմար է լուծել միջակայքերի եղանակով։ Դրա համար կարելի է կիրառել քայլերի հետևյալ հաջորդականությունը․

1. լուծել  f₁(x) = 0, f₂(x) = 0, … , fₙ(x) = 0 հավասարումները․ գտնված արմատները տրված հավասարման (անհավասարման) որոշման տիրույթը տրոհում են միջակայքերի, որոնցից յուրաքանչյուրում մոդուլատակ ֆունկցիաները պահպանում են նշանները։
2. բացել այդ ֆունկցիաների մոդուլները յուրաքանչյուր միջակայքի համար՝ հաշվի առնելով դիտարկվող միջակայքերում ֆունկցիաների նշանները։
3. օգտվելով հավասարումների և անհավասարումների հոդվածում վերոնշյալ լուծման եղանականերից՝ կազմել համակարգերի համախումբ և լուծել այն։

ax² + b|x| + c ≤ 0, ax² + b|x| + c ≥ 0 տեսքի անհավասարումների լուծումը։

Այս տեսքի անհավասարումները լուծելիս նախ պետք է նկատել, որ x² = |x|², որից հետո կարող ենք լուծել տրվածին համարժեք a|x|² + b|x| + c ≥ 0 

(կամ a|x|² + b|x| + c ≤ 0) անհավասարումը։

Պարզության համար |x| -ը կարող ենք նշանակել t -ով (t ≥ 0), որից հետո պետք է լուծենք ձևափոխված հետևյալ անհավասարումը t -ի նկատմամբ՝

at² + bt + c ≥ 0  (կամ at² + bt + c ≤ 0)

Ստացված քառակուսային անհավասարումը t -ի նկատմամբ լուծելուց հետո կստանանք, որ t∈(-∞ ; t₁]∪[t₂ ; +∞) (եթե ունի 2 տարբեր արմատ, t₁ < t₂) և t∈[t₁ ; t₂] (եթե ունի 2 տարբեր արմատ, t₁ < t₂):

Այնուհետև, պետք է հետ նշանակում կատարել t = |x| -ով, և կստանանք՝ 

a|x|² + b|x| + c ≥ 0 ⟶ |x| ≤ t₁ (թիվ է) կամ |x| ≥ t₂ (թիվ է)  (1) ;

a|x|² + b|x| + c ≤ 0 ⟶ |x| ≥ t₁ և |x| ≤ t₂  (2) :

(1) -ի համար կստանանք անհավասարումների համախումբ, իսկ (2) -ի համար՝ անհավասարումների համակարգ։ Վերջիններս լուծելով կստանանք տրված անհավասարումների լուծումների բազմությունները։ 

Շնորհակալություն ուշադրության համար