Կրճատ բազմապատկման բանաձևերը։ Ածանցյալ բանաձևերը

Ընթերցման ժամանակը՝ 7 րոպե

Բազմանդամների բազմապատկումը կարելի է ավելի կարճ կատարել, եթե օգտվենք կրճատ բազմապատկման բանաձևերից։ Դրանցից շատերը հանդիսանում են Նյուտոնի երկանդամի մասնավոր դեպքեր։ Նյուտոնի երկանդամ է կոչվում (a+b)ⁿ արտահայտությունը, որտեղ a -ն և b -ն կամայական թվեր են, իսկ n -ը՝ բնական։ Նյուտոնի երկանդամը «բացվում» է այսպես՝

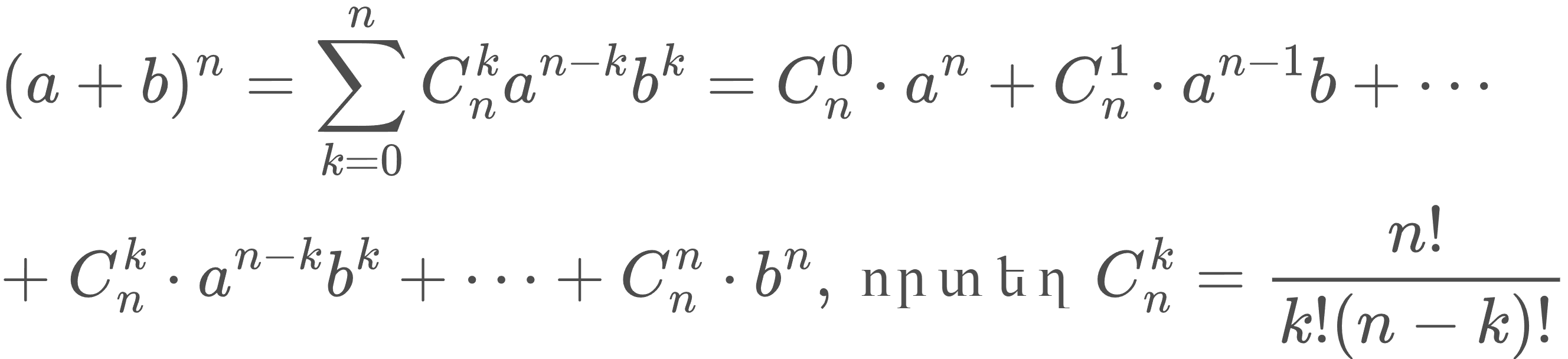
Բանաձևը անվանել են ի պատիվ անգլիացի մեծ գիտնական Իսահակ Նյուտոնի, քանի որ նա է այն ընդհանրացրել։ Նա առաջինն էր, ով հասկացավ, որ այս բանաձևը կարող է օգտագործվել ոչ միայն բնական, այլև բացասական և կոտորակային ցուցիչներով աստիճանների համար։ Նրանից առաջ արդեն հայտնի էր Պասկալի եռանկյունը, որից կարելի է ստանալ բնական ցուցիչով աստիճանների բինոմային գործակիցները, սակայն Նյուտոնը ընդլայնեց դրա կիրառումը։ Նա ապացուցեց բանաձևը ցանկացած իրական n թվի համար։

Կամայական a և b իրական թվերի համար ճիշտ են հետևյալ հավասարությունները․

Բանաձևեր քառակուսիների համար՝

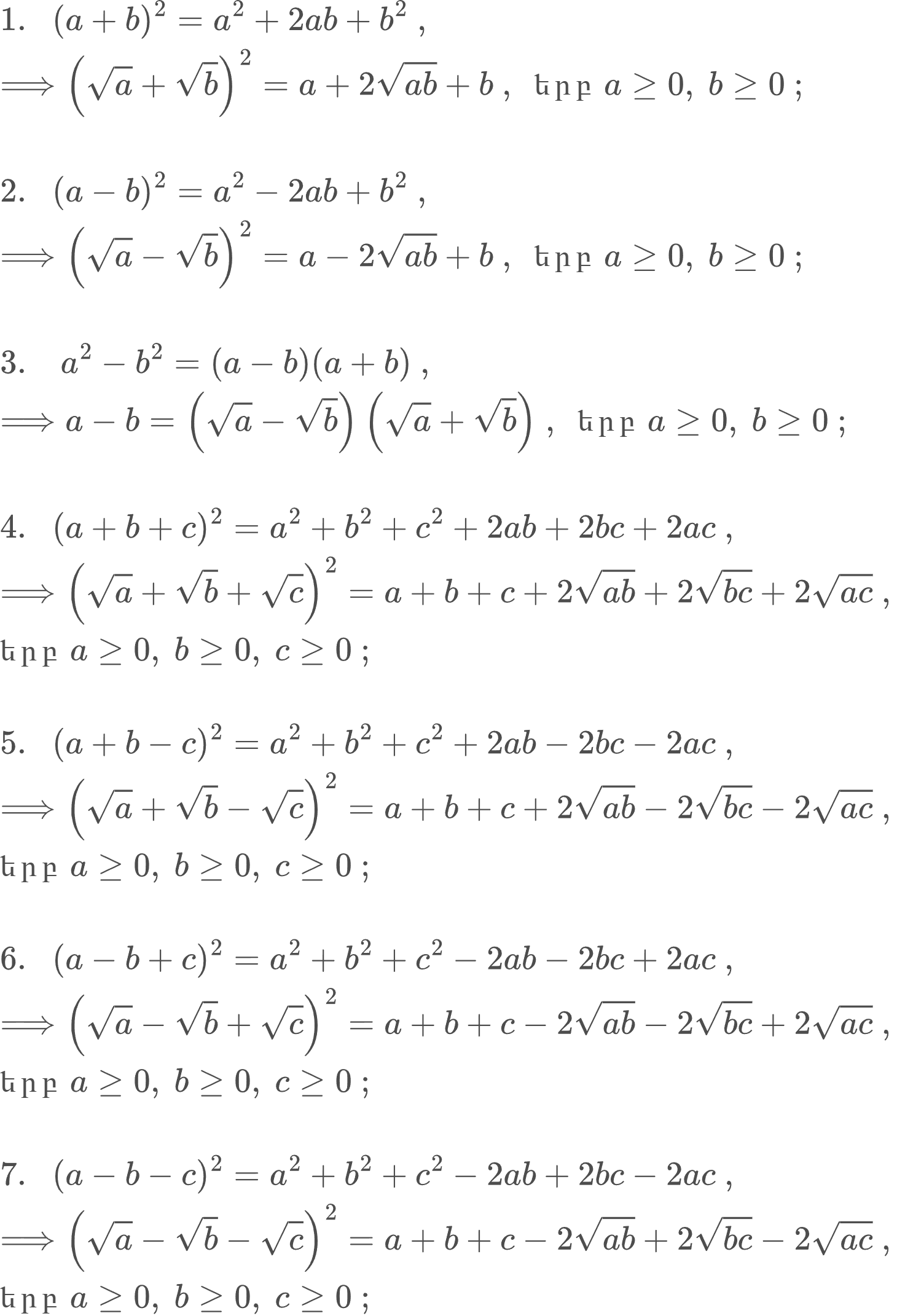
Բանաձևեր խորանարդների համար՝

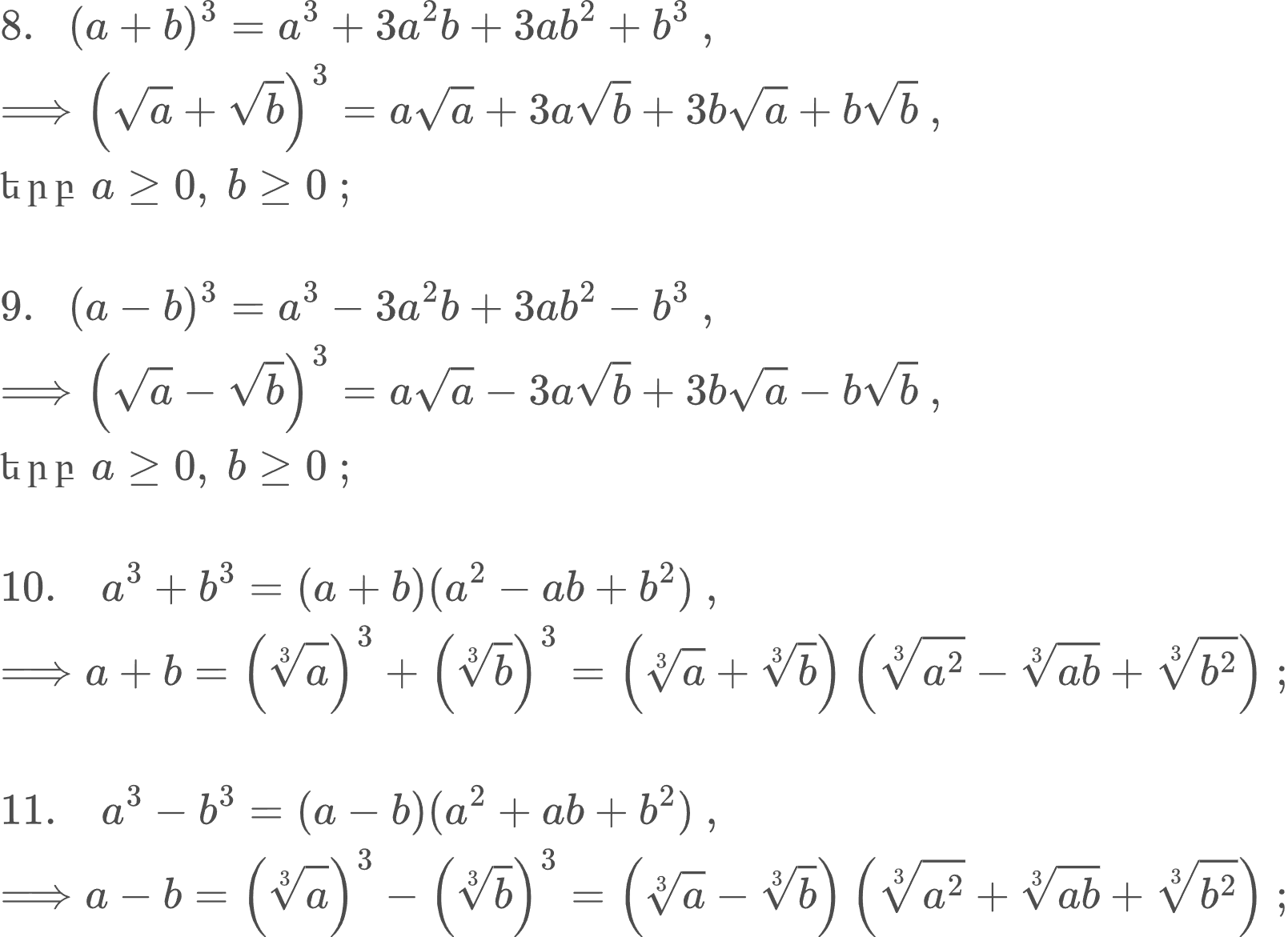
Բանաձևեր n -րդ աստիճանների համար՝

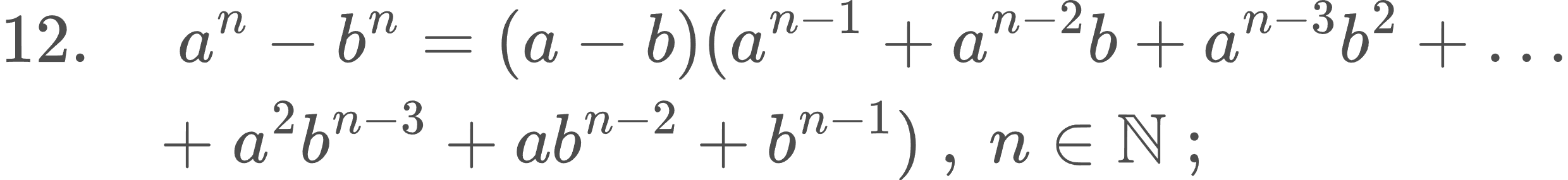
Զույգ աստիճանացույցերի դեպքում (n = 2k)՝

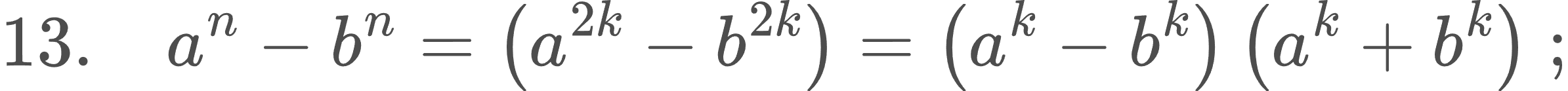
Կենտ աստիճանացույցերի դեպքում (n = 2k+1)՝

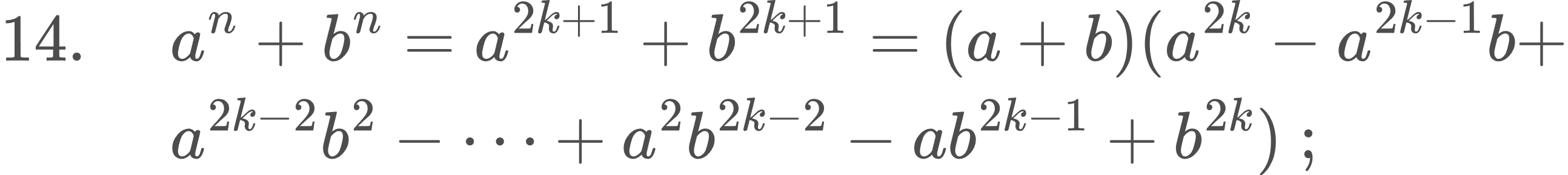
Ստորև բերված բանաձևը օգտակար է խորանարդ աստիճանի հավասարումներ լուծելու ժամանակ․

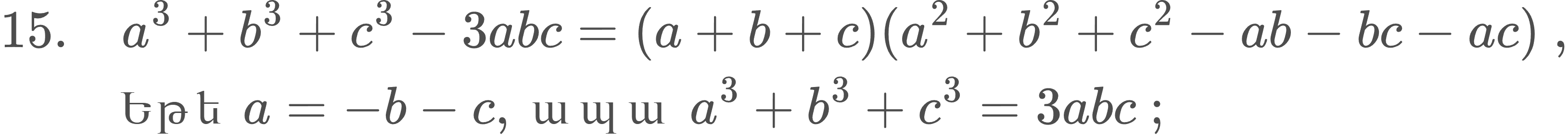
Որոշ կարևոր հատկություններ․

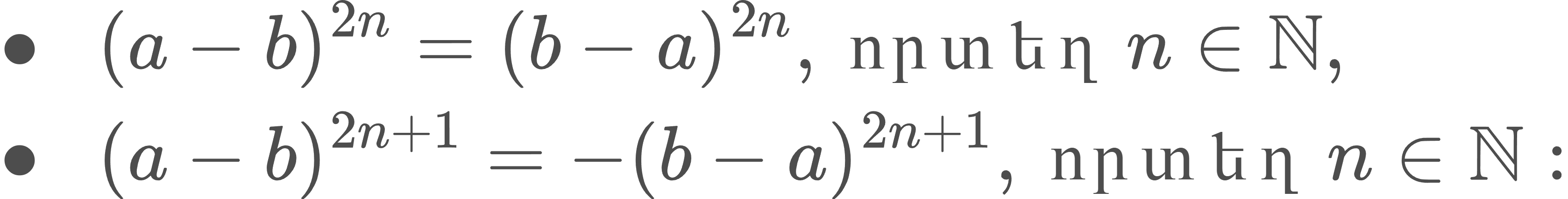
Շնորհակալություն ուշադրության համար