Պետական ավարտական և միասնական քննությունների ուղեցույց

Ընթերցման ժամանակը՝ 9 րոպե

Այս ուղեցույցում ներկայացված են 2024-2025 ուստարվա մաթեմատիկա առարկայից պետական ավարտական և միասնական քննությունների թեստերի կառուցվածքը և առաջադրանքների կառուցվածքային տիպերը։

Թեստի կառուցվածքը․

Քննական թեստը կազմված է Ա և Բ մակարդակներից և բաղկացած է 19 առաջադրանքից` իրենց ենթաառաջադրանքներով: Ա մակարդակի առաջադրանքները վերաբերում են ավարտական քննությանը: Միասնական քննության թեստը պարունակում է Ա և Բ մակարդակները:

Թեստային առաջադրանքներում ներառված են ենթառաջադրանքների 3 կառուցվածքային տեսակները` ընտրովի պատասխանով ենթառաջադրանքներ, կարճ պատասխանով ենթառաջադրանքներ և պնդումների փնջեր` յուրաքանչյուրը բաղկացած 6 պնդումից: Ընտրովի և կարճ պատասխանով ենթառաջադրանքներից յուրաքանչյուրին ճիշտ պատասխանելու դեպքում տրվում է 1 միավոր, պնդումների փնջին` առավելագույնը 6 միավոր:

Թեստի ընդհանուր միավորը 80 է: Միասնական քննական թեստի առաջադրանքների կատարման համար տրվում է 180 րոպե:

Բուհ ընդունվելու համար միասնական քննության միավորը հաշվարկվում է 20 միավորանոց սանդղակով` հիմնվելով ամբողջ աշխատանքի (Ա և Բ մակարդակների) կատարման արդյունքում դիմորդի հավաքած միավորների վրա:

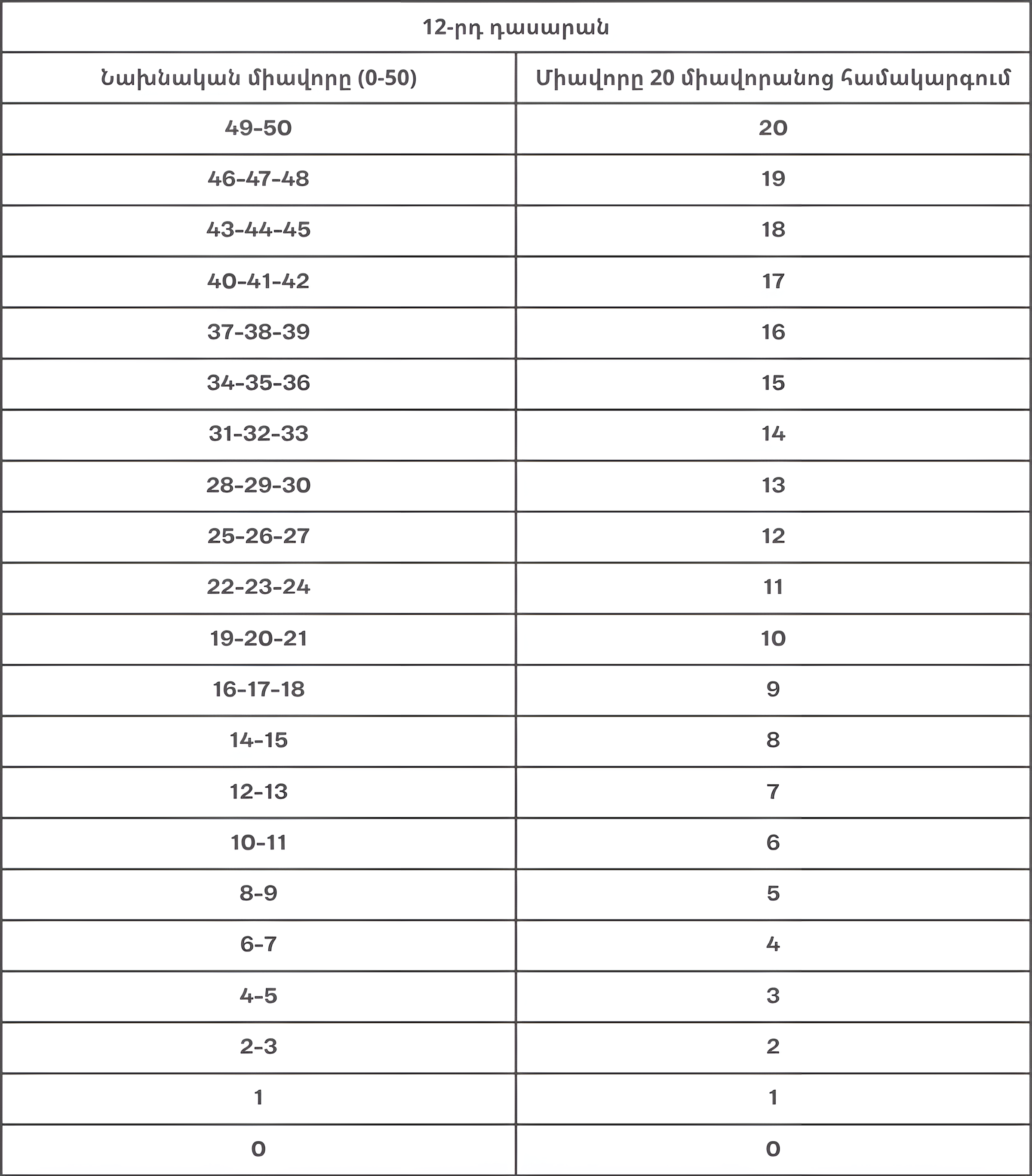
Դպրոցի շրջանավարտի ավարտական գնահատականը նույնպես որոշվում է 20 միավորանոց, հատուկ ավարտական մասի համար նախասեսված սանդղակով, որը բերված է ստորև․

Առաջադրանքների կառուցվածքային տեսակները․

1․ Ընտրովի պատասխանով առաջադրանքներ։

Տրվում է պատասխանի չորս տարբերակ, որոնցից միայն մեկն է ճիշտ:

Այդպիսի առաջադրանքի պատասխանն ընտրելիս շրջանավարտը համապատասխան համարով առաջադրանքի ուղղահայաց սյունակի պատասխանների հնարավոր չորս տարբերակների վանդակներից մեկում պետք է դնի «X» նշանը: Յուրաքանչյուր ճիշտ պատասխանի դիմաց կտրվի 1 միավոր։

2․ Կարճ պատասխանով առաջադրանքներ։

Այս առաջադրանքին պատասխանելիս անհրաժեշտ է գրել կարճ պատասխանը` նախատեսված հորիզոնական երեք վանդակներից յուրաքանչյուրում գրելով մեկ թվանշան: Առաջադրանքի պատասխան կարող է լինել 0-ից 999-ը ամբողջ թվերից որևէ մեկը (չափման միավորը չի նշվում): Այսպիսով՝ կարճ պատասխանով առաջադրանքների պատասխանները ոչ բացասական ամբողջ թվեր են: Յուրաքանչյուր ճիշտ պատասխանի դիմաց կտրվի 1 միավոր։

3․ Պնդումների փունջ։

Այս տիպի առաջադրանքներն ունեն հետևյալ բովանդակությունը․ տրված է որևէ մաթեմատիկական օբյեկտ (օրինակ` ֆունկցիա, հավասարում, երկրաչափական պատկեր և այլն),որի վերաբերյալ բերված է 6 պնդում։ Յուրաքանչյուրի համար շրջանավարտը պետք է պարզի` այն ճի՞շտ է, թե՞ սխալ է: Հարցին ճիշտ պատասխանելու դեպքում շրջանավարտը ստանում է 1 միավոր, իսկ սխալ պատասխանելու դեպքում փնջից դիմորդի հավաքած միավորից հանվում է 1 միավոր: Շրջանավարտը հնարավորություն ունի պատասխանելու «Չգիտեմ»: Այդ դեպքում տվյալ պնդման համար նրա պատասխանը գնահատվում է 0 միավոր: Եթե առաջադրանքի 6 պնդումներից ստացված միավորների գումարը դրական է, այն համարվում է այդ առաջադրանքի գնահատականը: Հակառակ դեպքում, այսինքն` երբ միավորների գումարը 0 է կամ բացասական, առաջադրանքի գնահատականը 0 է։

Այս տիպի առաջադրանքներին պատասխանելիս «X» նշանը անհրաժեշտ է դնել պնդման ուղղահայաց սյունակի պատասխանների հնարավոր երեք` «Ճիշտ է», «Սխալ է», «Չգիտեմ» պնդումների վանդակներից մեկում: Պնդման պատասխանը համարվում է ճիշտ, եթե պնդումը ճշմարիտ է և շրջանավարտը նշել է «Ճիշտ է» պատասխանը, կամ եթե պնդումը ճշմարիտ չէ և շրջանավարտը նշել է «Սխալ է» պատասխանը:

Վերոնշյալ փաստերը հաշվի առնելով՝ պարզ է դառնում, որ ընտրովի պատասխանով և կարճ պատասխանով յուրաքանչյուր առաջադրանքին ճիշտ պատասխանելու դեպքում տրվում է 1 միավոր։ Իրավիճակը այլ է պնդումների փնջի առաջադրանքների համար։

Ճիշտ է, ամեն այդպիսի առաջադրանքի յուրաքանչյուր պնդման ճիշտ պատասխանելու դեպքում տրվում է 1 միավոր, բայց յուրաքանչյուր պնդման սխալ պատասխանելու դեպքում ոչ թե միավոր չի տրվում, այլ հանվում է։ Միավոր չի հանվի միայն այն դեպքում, եթե որպես պատասխան «X» նշանը դրվի «Չգիտեմ» պնդմանը համապատասխանող վանդակում։ Այսինքն՝

• եթե 6 պնդումներից 6-ին էլ տրվի ճիշտ պատասխան, կստանանք ամբողջական 6 միավոր։
• Եթե 6-ից 5-ին տրվի ճիշտ պատասխան, ոչ թե կստանանք 5 ⋅ 1 = 5 միավոր, այլ 1 միավոր էլ կհանվի սխալ պատասխանած պնդման դիմաց, այսինքն՝ կստանանք + 5 - 1 = 4 միավոր։
• Եթե 6-ից 4-ին տրվի ճիշտ պատասխան, ոչ թե կստանանք 4 ⋅ 1 = 4 միավոր, այլ 2 միավոր էլ կհանվի սխալ պատասխանած պնդումների դիմաց, այսինքն՝ կստանանք + 4 - 2 = 2 միավոր։
• Եթե 6-ից 3-ին տրվի ճիշտ պատասխան, ոչ թե կստանանք 3 ⋅ 1 = 3 միավոր, այլ 3 միավոր էլ կհանվի սխալ պատասխանած պնդումների դիմաց, այսինքն՝ կստանանք + 3 - 3 = 0 միավոր։

Եթե պնդումների քանակի կեսից (6-ի կեսը 3 է) պակաս պնդումներին տրվի ճիշտ պատասխան, ապա հաշվարկների արդյունքնում կստանանք բացասական թիվ։ Հաշվի առնելով, որ միավորների գումարի 0 կամ բացասական լինելու դեպքում առաջադրանքը գնահատվում է 0 միավոր, կարող ենք եզրակացնել, որ 3 կամ պակաս պնդման ճիշտ պատասխանելու դեպքում այդ առաջադրանքի դիմաց կստանանք 0։

Քանի որ թեստի ընդհանուր միավորը 80 է, բայց միասնական քննության միավորը հաշվարկվում է 20 միավորանոց սանդղակով, թեստից մեր ստացած գնահատականը պարզելու համար յուրաքանչյուր առաջադրանքից ստացված միավորը պետք է բաժանենք 4-ի՝ հետևյալ ձևով․

• Եթե ընտրովի պատասխանով որևէ առաջադրանքին ճիշտ ենք պատասխանել => 1 միավոր => 1 ։ 4 = 0,25 միավոր ;
• Եթե կարճ պատասխանով որևէ առաջադրանքին ճիշտ ենք պատասխանել => 1 միավոր => 0,25 միավոր ;
• Եթե պնդումների փնջի որևէ առաջադրանքի 6 պնդումներից 6-ին էլ ճիշտ ենք պատասխանել => 6 միավոր => 6 : 4 = 1,5 միավոր ;
• Եթե պնդումների փնջի որևէ առաջադրանքի 6 պնդումներից 5-ին ճիշտ ենք պատասխանել => 4 միավոր => 4 : 4 = 1 միավոր ;
• Եթե պնդումների փնջի որևէ առաջադրանքի 6 պնդումներից 4-ին ճիշտ ենք պատասխանել => 2 միավոր => 2 : 4 = 0,5 միավոր ;
• Եթե պնդումների փնջի որևէ առաջադրանքի 6 պնդումներից 3-ին կամ 3-ից պակասին (2, 1, կամ 0) ճիշտ ենք պատասխանել => 0 միավոր ։

Կարծում եմ՝ հիմա բոլորին պարզ դարձավ, թե ինչպես ճիշտ հաշվարկել մաթեմատիկա առարկայից միասնական քննության թեստի գնահատականը։

Հոդվածը ստեղծվել է «Գնահատման և թեստավորման կենտրոն»-ի ուղեցույցը հիմք ընդունելով։

Շնորհակալություն ուշադրության համար